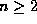is prime if and only if n divides
.
Gauss (Disquisitiones Arithmeticae, 1801, art. 329) wrote:
The problem of distinguishing prime numbers from composite numbers ... is known to be one of the most important and useful in arithmetic. ... The dignity of the science itself seems to require that every possible means be explored for the solution of a problem so elegant and so celebrated.
In 1773 Lagrange observed that Wilson's Theorem could be used to identify primes by writing it in the form
An integer 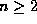is prime if and only if n divides
.
In connection with the solution of Hilbert's Tenth Problem, Matijasevic
(1971) constructed an integer polynomial f (in many variables)
such that the set of positive values of f is exactly the set of
prime numbers (see here for an elegant construction).
The construction is based on Lagrange's reformulation of Wilson's Theorem.
Professor J.P. Jones has asked whether a similar criteria to identify
primes can be obtained from Wolstenholme's congruence: that is,
whether it is true that (4) holds if and only if p is a prime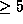 
.
(R. McIntosh has shown that the
congruence can hold 
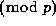for composite 
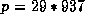and even
for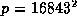 
; thus the `3' is certainly necessary.)
One might also ask the same question based on the generalization (5)
of Wolstenholme's Theorem, or of (6).
As far back as 1819, Babbage gave an easily proved characterization of the primes, based on a number of simultaneous congruences:
An integer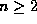 
is prime if and only if 
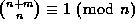for all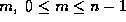 
(notice that the range for m may be shortened to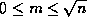 
).
In 1972, Mann and Shanks came up with another characterization involving a number of simultaneous congruences:
An integer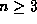 
is prime if and only if m divides
for all 
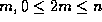
(notice that the range for m may be shortened to 
). To prove this note first that if n is prime then
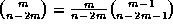, which is
clearly divisible by m, as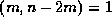 
.
On the other hand, if even n is composite
take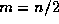 
so that m does not divide 
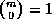, and
if odd n is composite and divisible by prime p take 
.
If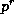 
is the highest
power of p that divides m (note that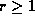 
) then it is easy to
show that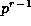 
is the highest power of p that divides 
,
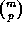by Kummer's Theorem.
In 1915 Fleck gave an imaginative generalization of Wilson's Theorem, that can be used to characterize primes after a certain amount of trial division:
For any integers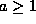 
and n, free of prime factors 
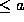, we have
that n is prime if and only if
<
(23)
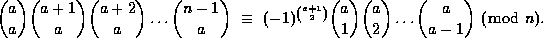
(Actually Fleck did not include the condition that n is free
of prime factors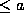 
but some such condition is essential as
(23) holds for the example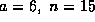 
.)
To see this, note first that if n is composite with prime factor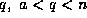 
,
then q divides the left side of (23) (as q divides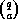 
),
but not the right side. On the other hand suppose that n=p is prime.
We prove (23) for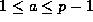 
by induction on a:
For a=1 this is just Wilson's Theorem.
Thereafter, the ratio of (23) for a+1 to (23) for a, is
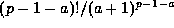on the left side and 
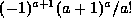on the right side, which are congruent, modulo p, by Fermat's Theorem
and Wilson's Theorem.