is given by the number of `carries' when we
add m and n-m in base p.
Many great mathematicians of the nineteenth century considered problems involving binomial coefficients modulo a prime power (for instance Babbage, Cauchy, Cayley, Gauss, Hensel, Hermite, Kummer, Legendre, Lucas and Stickelberger -- see Dickson). They discovered a variety of elegant and surprising Theorems which are often easy to prove. In this article we shall exhibit most of these results, and extend them in a variety of ways. We start with a discussion of what this article contains:
In 1852 Kummer showed that the power of prime p that divides the binomial
coefficient is given by the number of `carries' when we
add m and n-m in base p.
In 1878 Lucas gave a method to easily determine
the value of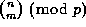 
: Let 
and 
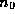be the least
non-negative residues of m and 
, respectively. Then
where, as usual,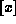 
denotes the largest integer 
,
and we use the convention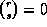 
if r<s.
Re-writing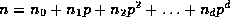 
and
in base p
(so that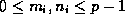 
for each i), this may also be expressed
as
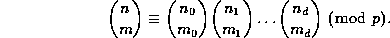
We will give three very different proofs of Lucas' Theorem: via number theory, via cellular automata, and via the combinatorics of power series.
Note that if p divides
then (1) follows easily from Kummer's
Theorem. However, if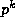 
is the exact power of p dividing 
,
then we might ask for the value of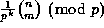 
.
This is given by a result discovered by each of Anton (1869),
Stickelberger (1890) and Hensel (1902) (and many others since !), which
shows that
where r = n-m. Numerous authors have asked whether there is an analogous
formula, modulo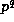 
, for arbitrary 
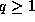. In section 2 we show
the following:
For a given integer n define 
to be the product of those integers
that are not divisible by p.
Theorem 1. Suppose that prime power
where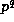 
and positive integers
m=n+r are given. Let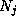 
be the least positive residue of 
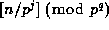for each 
(and
make the corresponding definitions for m and r).
Let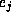 
be the number of `carries', when adding m and r in base p,
on or beyond the jth digit). Then
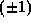is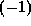 
except if p=2 and 
.
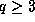Taking q=1 in (3) gives (2).
Note that (3) may be re-written in terms of
factorials, since each 
.
A similar result appears in
Davis and Webb .
Theorem 1 provides a quick way to compute the value of binomial
coefficients modulo arbitrary prime powers: in fact
we will show
that this takes just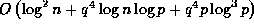 
elementary operations.
Wilson's Theorem (which was actually discovered by Liebnitz)
states that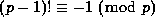 
for all primes
p. An easy consequence of this is that
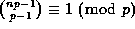for all integers n.
In 1819 Babbage noticed that, further,
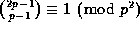for all primes 
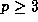, and
Wolstenholme, in 1862, that
for all primes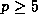 
.
In 1952 Ljunggren generalized this to
;
and Jacobsthal to
for any integers n>m>0 and prime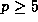 
, where q
is the power of p dividing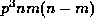 
(this exponent q can only be increased if p divides 
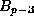, the
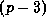rd Bernoulli number).
These results, as well as many other similar congruences with larger
exponents q, follow easily from Proposition 5 below. For example,
if prime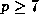 
then
Ljunggren's result above may be re-written as
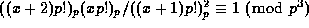for any
integer
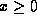and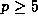 
. Proposition 5 implies the generalization
unless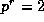 
, or 2r+1 = p or 
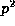, when the congruence holds
.
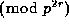Another generalization of Wolstenholme's congruence is given by
Theorem 2. Suppose that prime p and positive integers
u and r are given. Then
except if
or 2r+1 = p or 
,
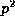when the congruence holds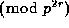 
,
where `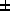
' can only be `-' if p=2 (which is easily determined
by evaluating both sides of (8) modulo 4), and the integer
Note how Theorem 2 allows us to express any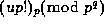 
in terms of 
with 
. In Theorem 3 below we prove
a similar result for any factorial, which allows us to compute such factorials
very rapidly.
In 1899 Glaisher observed that the number of odd entries in any given
row of Pascal's Triangle is a power of 2. This follows from Kummer's
Theorem by noting that 
is odd if and only if there
are no carries when adding m and n-m in base 2; in other words that
the digits `1' in the binary expansion of m are a subset of those in the
binary expansion of n. Clearly if there are k digits `1' in the
binary expansion of n, then there are 
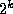possible subsets of these
`1's, and each corresponds to a value of m -- thus there are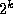 
odd entries in the nth row of Pascal's Triangle.
Larry Roberts also has an elegant (unpublished) result, depending on
Kummer's Theorem: Let 
be the binary number whose mth digit
is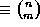 
modulo 2; in other words, the integer formed
by reading the nth row of Pascal's Triangle, modulo 2, from left to right.
Then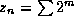 
, where the sum is over those values of m, for
which the digits `1' in its binary expansion are a subset of those of n.
Thus if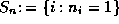 
then
where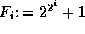 
is the ith Fermat number.
In section 5 we give somewhat different proofs of these results, and of Lucas' Theorem, using cellular automata.
In a recent paper , using methods from both elementary number theory
and the theory of cellular automata, we extended this result of
Glaisher's to the entries in Pascal's triangle that are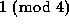 
:
specifically we showed that in any given row of Pascal's triangle,
the number of entries that are congruent to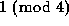 
is either
0 or a power of 2. Similarly for 
.
We then extended this to 
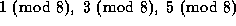and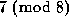 
.
The likelihood of a general result of this type begins to emerge, and
to find out more the reader is encouraged to look at
my paper .
As is so well known, for any fixed n,
the sum, over all m, of the binomial coefficients
, is exactly
2 to the power n. What is less well-known is that the
sum of the binomial coefficients, over all m in certain fixed
residue classes, sometimes satisfy certain
surprising congruences.
In 1895 Morley showed that for any prime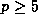 
,
His ingenious proof, which is based on an explicit form of
De Moivre's Theorem, can be modified
to show that (14) holds modulo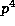 
if and only if p divides 
;
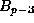however it cannot be modified to investigate other binomial coefficients,
and so we use different method for this in section 9. Our first result is
that
for any 
: In fact, this product is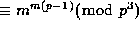 
whenever the p-2nd Bernoulli polynomial vanishes 
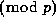at
(which is immediate for m=2).
In 1938 Emma Lehmer related the values of
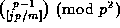, for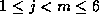 
, to
Fermat's Last Theorem for exponent p. We shall show, in section 9, that
recent, as yet unpublished, results of Skula and Cui-Xiang imply that if
the first case of Fermat's Last Theorem is false for prime exponent p
(that is, there exist integers a, b, c, not divisible by p, for which
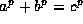) then
for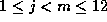 
; moreover, Skula'a approach implies that the `12'
here may be changed to any given number after a finite amount of computation.
There are many results in the literature that relate the value
of binomial coefficients of the form
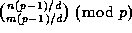, for a given, fixed d>0
dividing p-1, to representations of the prime p by certain quadratic
forms (see Hudson and Williams). The first such result, due to Gauss (1828), is for d=4: \
Write any prime 
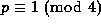as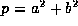 
, and choose
the sign of a so that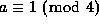 
; then
.
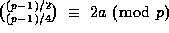Recently, Beukers conjectured that
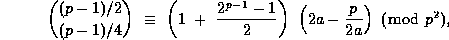
and this was proved by Chowla, Dwork and Evans.
In 1846, Jacobi showed that if we write any prime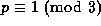 
as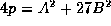 
, where the sign of A is chosen so that
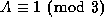, then
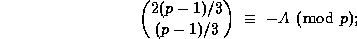
and this has now been shown to be 
These congruences, modulo 
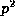, have only been discovered quite
recently and there are presumably many others waiting to be found.
