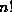is
In 1808 Legendre showed that the exact power of p dividing 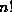is
Writing n in base p as above, we define the sum of digits function
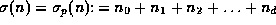. Then (17)
equals
) then clearly p does not divide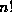 
and both (17) and
(18) equal zero. So, given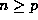 
, note that the set of integers 
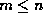that are divisible by p are precisely the set of integers pk for
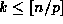. Thus the power of p dividing 
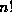is exactly 
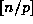plus the power of p dividing 
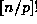. (17) then follows immediately
from the induction hypothesis, and (18) after noting that
.
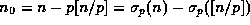