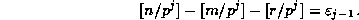
if there is a `carry' in the jth digit when we add m and r in base p; otherwise let
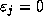(including 
).
We observed, in the proof of Kummer's Theorem that, for each integer
,
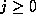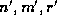be the least residues, in absolute
value, of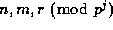 
, respectively, so that 
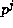times the
left side of (19), plus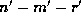 
equals n-m-r = 0. However,
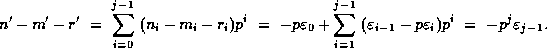
and (19) follows.