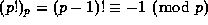Wilson's Theorem for prime powers

(The Proof of Lemma 1 and its Corollary)

Wilson's Theorem, states that 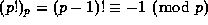. We generalize it, to prime powers, as follows:

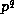Lemma 1 For any given prime power we have

where 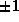is -1, unless 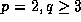in which case 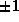is 1.

Proof:
Pair up each m in the product with its inverse

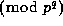to see that

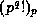is congruent, modulo

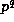, to the product of those

that are not distinct from their inverses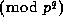

; that is those m for which

. It is easy to show that the only such m are 1 and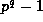

unless

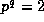(when one only has m=1) or

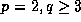when one has the additional solutions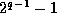

and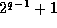

. The result then follows.

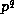Corollary 1 For any given prime power , let 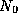be the least non-negative residue of . Then

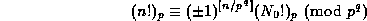
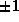where is as in Lemma 1.

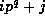Proof: We write each r in the product below as

, to get

(20)

by Lemma 1, where 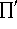signifies a product over integers not divisible by p.